Clustering is a fundamental, ubiquitous problem in data mining and unsupervised machine learning, where the goal is to group together similar items. The standard forms of clustering are metric clustering and graph clustering. In metric clustering, a given metric space defines distances between data points, which are grouped together based on their separation. In graph clustering, a given graph connects similar data points through edges, and the clustering process groups data points together based on the connections between them. Both clustering forms are particularly useful for large corpora where class labels can’t be defined. Examples of such corpora are the ever-growing digital text collections of various internet platforms, with applications including organizing and searching documents, identifying patterns in text, and recommending relevant documents to users (see more examples in the following posts: clustering related queries based on user intent and practical differentially private clustering).
The choice of text clustering method often presents a dilemma. One approach is to use embedding models, such as BERT or RoBERTa, to define a metric clustering problem. Another is to utilize cross-attention (CA) models, such as PaLM or GPT, to define a graph clustering problem. CA models can provide highly accurate similarity scores, but constructing the input graph may require a prohibitive quadratic number of inference calls to the model. On the other hand, a metric space can efficiently be defined by distances of embeddings produced by embedding models. However, these similarity distances are typically of substantial lower-quality compared to the similarity signals of CA models, and hence the produced clustering can be of much lower-quality.
 |  |
| An overview of the embedding-based and cross-attention–based similarity scoring functions and their scalability vs. quality dilemma. |
Motivated by this, in “KwikBucks: Correlation Clustering with Cheap-Weak and Expensive-Strong Signals”, presented at ICLR 2023, we describe a novel clustering algorithm that effectively combines the scalability benefits from embedding models and the quality from CA models. This graph clustering algorithm has query access to both the CA model and the embedding model, however, we apply a budget on the number of queries made to the CA model. This algorithm uses the CA model to answer edge queries, and benefits from unlimited access to similarity scores from the embedding model. We describe how this proposed setting bridges algorithm design and practical considerations, and can be applied to other clustering problems with similar available scoring functions, such as clustering problems on images and media. We demonstrate how this algorithm yields high-quality clusters with almost a linear number of query calls to the CA model. We have also open-sourced the data used in our experiments.
The clustering algorithm
The KwikBucks algorithm is an extension of the well-known KwikCluster algorithm (Pivot algorithm). The high-level idea is to first select a set of documents (i.e., centers) with no similarity edge between them, and then form clusters around these centers. To obtain the quality from CA models and the runtime efficiency from embedding models, we introduce the novel combo similarity oracle mechanism. In this approach, we utilize the embedding model to guide the selection of queries to be sent to the CA model. When given a set of center documents and a target document, the combo similarity oracle mechanism outputs a center from the set that is similar to the target document, if present. The combo similarity oracle enables us to save on budget by limiting the number of query calls to the CA model when selecting centers and forming clusters. It does this by first ranking centers based on their embedding similarity to the target document, and then querying the CA model for the pair (i.e., target document and ranked center), as shown below.
 |
| A combo similarity oracle that for a set of documents and a target document, returns a similar document from the set, if present. |
We then perform a post processing step to merge clusters if there is a strong connection between two of them, i.e., when the number of connecting edges is higher than the number of missing edges between two clusters. Additionally, we apply the following steps for further computational savings on queries made to the CA model, and to improve performance at runtime:
- We leverage query-efficient correlation clustering to form a set of centers from a set of randomly selected documents instead of selecting these centers from all the documents (in the illustration below, the center nodes are red).
- We apply the combo similarity oracle mechanism to perform the cluster assignment step in parallel for all non-center documents and leave documents with no similar center as singletons. In the illustration below, the assignments are depicted by blue arrows and initially two (non-center) nodes are left as singletons due to no assignment.
- In the post-processing step, to ensure scalability, we use the embedding similarity scores to filter down the potential mergers (in the illustration below, the green dashed boundaries show these merged clusters).
 |
| Illustration of progress of the clustering algorithm on a given graph instance. |
Results
We evaluate the novel clustering algorithm on various datasets with different properties using different embedding-based and cross-attention–based models. We compare the clustering algorithm’s performance with the two best performing baselines (see the paper for more details):
- The query-efficient correlation clustering algorithm for budgeted clustering with access to CA only.
- Spectral clustering on the k-nearest neighbor graph (kNN) formed by querying the CA model for the k-nearest neighbors of each vertex from embedding-based similarity.
To evaluate the quality of clustering, we use precision and recall. Precision is used to calculate the percentage of similar pairs out of all co-clustered pairs and recall is the percentage of co-clustered similar pairs out of all similar pairs. To measure the quality of the obtained solutions from our experiments, we use the F1-score, which is the harmonic mean of the precision and recall, where 1.0 is the highest possible value that indicates perfect precision and recall, and 0 is the lowest possible value that indicates if either precision or recall are zero. The table below reports the F1-score for Kwikbucks and various baselines in the case that we allow only a linear number of queries to the CA model. We show that Kwikbucks offers a substantial boost in performance with a 45% relative improvement compared to the best baseline when averaging across all datasets.
 |
| Comparing the clustering algorithm to two baseline algorithms using various public datasets: (1) The query-efficient correlation clustering algorithm for budgeted clustering with access to CA only, and (2) spectral clustering on the k-nearest neighbor (kNN) graph formed by querying the CA model for the k-nearest neighbors of each vertex from embedding-based similarity. Pre-processed datasets can be downloaded here. |
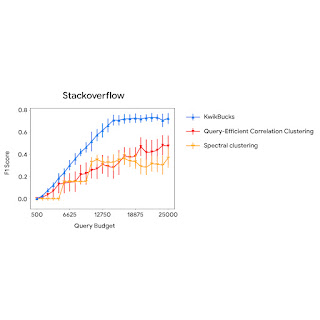
The figure below compares the clustering algorithm’s performance with baselines using different query budgets. We observe that KwikBucks consistently outperforms other baselines at various budgets.
 |
| A comparison of KwikBucks with top-2 baselines when allowed different budgets for querying the cross-attention model. |
Conclusion
Text clustering often presents a dilemma in the choice of similarity function: embedding models are scalable but lack quality, while cross-attention models offer quality but substantially hurt scalability. We present a clustering algorithm that offers the best of both worlds: the scalability of embedding models and the quality of cross-attention models. KwikBucks can also be applied to other clustering problems with multiple similarity oracles of varying accuracy levels. This is validated with an exhaustive set of experiments on various datasets with diverse properties. See the paper for more details.
Acknowledgements
This project was initiated during Sandeep Silwal’s summer internship at Google in 2022. We would like to express our gratitude to our co-authors, Andrew McCallum, Andrew Nystrom, Deepak Ramachandran, and Sandeep Silwal, for their valuable contributions to this work. We also thank Ravi Kumar and John Guilyard for assistance with this blog post.