Every byte and every operation matters when trying to build a faster model, especially if the model is to run on-device. Neural architecture search (NAS) algorithms design sophisticated model architectures by searching through a larger model-space than what is possible manually. Different NAS algorithms, such as MNasNet and TuNAS, have been proposed and have discovered several efficient model architectures, including MobileNetV3, EfficientNet.
Here we present LayerNAS, an approach that reformulates the multi-objective NAS problem within the framework of combinatorial optimization to greatly reduce the complexity, which results in an order of magnitude reduction in the number of model candidates that must be searched, less computation required for multi-trial searches, and the discovery of model architectures that perform better overall. Using a search space built on backbones taken from MobileNetV2 and MobileNetV3, we find models with top-1 accuracy on ImageNet up to 4.9% better than current state-of-the-art alternatives.
Problem formulation
NAS tackles a variety of different problems on different search spaces. To understand what LayerNAS is solving, let’s start with a simple example: You are the owner of GBurger and are designing the flagship burger, which is made up with three layers, each of which has four options with different costs. Burgers taste differently with different mixtures of options. You want to make the most delicious burger you can that comes in under a certain budget.
 |
| Make up your burger with different options available for each layer, each of which has different costs and provides different benefits. |
Just like the architecture for a neural network, the search space for the perfect burger follows a layerwise pattern, where each layer has several options with different changes to costs and performance. This simplified model illustrates a common approach for setting up search spaces. For example, for models based on convolutional neural networks (CNNs), like MobileNet, the NAS algorithm can select between a different number of options — filters, strides, or kernel sizes, etc. — for the convolution layer.
Method
We base our approach on search spaces that satisfy two conditions:
- An optimal model can be constructed using one of the model candidates generated from searching the previous layer and applying those search options to the current layer.
- If we set a FLOP constraint on the current layer, we can set constraints on the previous layer by reducing the FLOPs of the current layer.
Under these conditions it is possible to search linearly, from layer 1 to layer n knowing that when searching for the best option for layer i, a change in any previous layer will not improve the performance of the model. We can then bucket candidates by their cost, so that only a limited number of candidates are stored per layer. If two models have the same FLOPs, but one has better accuracy, we only keep the better one, and assume this won’t affect the architecture of following layers. Whereas the search space of a full treatment would expand exponentially with layers since the full range of options are available at each layer, our layerwise cost-based approach allows us to significantly reduce the search space, while being able to rigorously reason over the polynomial complexity of the algorithm. Our experimental evaluation shows that within these constraints we are able to discover top-performance models.
NAS as a combinatorial optimization problem
By applying a layerwise-cost approach, we reduce NAS to a combinatorial optimization problem. I.e., for layer i, we can compute the cost and reward after training with a given component Si . This implies the following combinatorial problem: How can we get the best reward if we select one choice per layer within a cost budget? This problem can be solved with many different methods, one of the most straightforward of which is to use dynamic programming, as described in the following pseudo code:
while True: # select a candidate to search in Layer i candidate = select_candidate(layeri) if searchable(candidate): # Use the layerwise structural information to generate the children. children = generate_children(candidate) reward = train(children) bucket = bucketize(children) if memorial_table[i][bucket] < reward: memorial_table[i][bucket] = children move to next layer |
| Pseudocode of LayerNAS. |
 |
| Illustration of the LayerNAS approach for the example of trying to create the best burger within a budget of $7–$9. We have four options for the first layer, which results in four burger candidates. By applying four options on the second layer, we have 16 candidates in total. We then bucket them into ranges from $1–$2, $3–$4, $5–$6, and $7–$8, and only keep the most delicious burger within each of the buckets, i.e., four candidates. Then, for those four candidates, we build 16 candidates using the pre-selected options for the first two layers and four options for each candidate for the third layer. We bucket them again, select the burgers within the budget range, and keep the best one. |
Experimental results
When comparing NAS algorithms, we evaluate the following metrics:
- Quality: What is the most accurate model that the algorithm can find?
- Stability: How stable is the selection of a good model? Can high-accuracy models be consistently discovered in consecutive trials of the algorithm?
- Efficiency: How long does it take for the algorithm to find a high-accuracy model?
We evaluate our algorithm on the standard benchmark NATS-Bench using 100 NAS runs, and we compare against other NAS algorithms, previously described in the NATS-Bench paper: random search, regularized evolution, and proximal policy optimization. Below, we visualize the differences between these search algorithms for the metrics described above. For each comparison, we record the average accuracy and variation in accuracy (variation is noted by a shaded region corresponding to the 25% to 75% interquartile range).
NATS-Bench size search defines a 5-layer CNN model, where each layer can choose from eight different options, each with different channels on the convolution layers. Our goal is to find the best model with 50% of the FLOPs required by the largest model. LayerNAS performance stands apart because it formulates the problem in a different way, separating the cost and reward to avoid searching a significant number of irrelevant model architectures. We found that model candidates with fewer channels in earlier layers tend to yield better performance, which explains how LayerNAS discovers better models much faster than other algorithms, as it avoids spending time on models outside the desired cost range. Note that the accuracy curve drops slightly after searching longer due to the lack of correlation between validation accuracy and test accuracy, i.e., some model architectures with higher validation accuracy have a lower test accuracy in NATS-Bench size search.
 |
 |
 |
| Top: NATS-Bench size search test accuracy on Cifar10; Middle: On Cifar100; Bottom: On ImageNet16-120. Average on 100 runs compared with random search (random), Regularized Evolution (evolution), and Proximal Policy Optimization (PPO). |
We construct search spaces based on MobileNetV2, MobileNetV2 1.4x, MobileNetV3 Small, and MobileNetV3 Large and search for an optimal model architecture under different #MADDs (number of multiply-additions per image) constraints. Among all settings, LayerNAS finds a model with better accuracy on ImageNet. See the paper for details.
 |
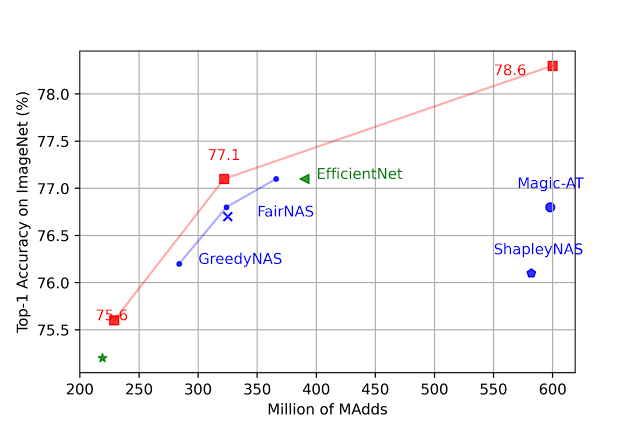| Comparison on models under different #MAdds. |
Conclusion
In this post, we demonstrated how to reformulate NAS into a combinatorial optimization problem, and proposed LayerNAS as a solution that requires only polynomial search complexity. We compared LayerNAS with existing popular NAS algorithms and showed that it can find improved models on NATS-Bench. We also use the method to find better architectures based on MobileNetV2, and MobileNetV3.
Acknowledgements
We would like to thank Jingyue Shen, Keshav Kumar, Daiyi Peng, Mingxing Tan, Esteban Real, Peter Young, Weijun Wang, Qifei Wang, Xuanyi Dong, Xin Wang, Yingjie Miao, Yun Long, Zhuo Wang, Da-Cheng Juan, Deqiang Chen, Fotis Iliopoulos, Han-Byul Kim, Rino Lee, Andrew Howard, Erik Vee, Rina Panigrahy, Ravi Kumar and Andrew Tomkins for their contribution, collaboration and advice.