Sequential A/B Testing Keeps the World Streaming Netflix Part 2: Counting Processes
Michael Lindon, Chris Sanden, Vache Shirikian, Yanjun Liu, Minal Mishra, Martin Tingley

Have you ever encountered a bug while streaming Netflix? Did your title stop unexpectedly, or not start at all? In the first installment of this blog series on sequential testing, we described our canary testing methodology for continuous metrics such as play-delay. One of our readers commented
What if the new release is not related to a new play/streaming feature? For example, what if the new release includes modified login functionality? Will you still monitor the “play-delay” metric?
Netflix monitors a large suite of metrics, many of which can be classified as counts. These include metrics such as the number of logins, errors, successful play starts, and even the number of customer call center contacts. In this second installment, we describe our sequential methodology for testing count metrics, outlined in the NeurIPS paper Anytime Valid Inference for Multinomial Count Data.
Spot the Difference
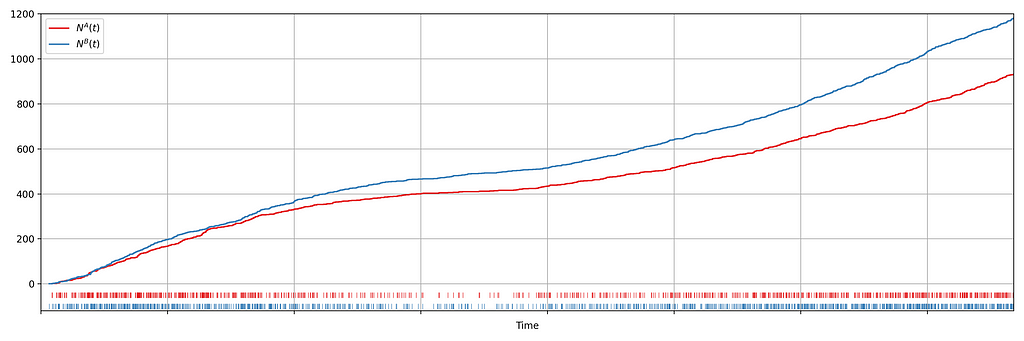
Suppose we are about to deploy new code that changes the login behavior. To de-risk the software rollout we A/B test the new code, known also as a canary test. Whenever an event such as a login occurs, a log flows through our real-time backend and the corresponding timestamp is recorded. Figure 1 illustrates the sequences of timestamps generated by devices assigned to the new (treatment) and existing (control) software versions. A question that naturally concerns us is whether there are fewer login events in the treatment. Can you tell?
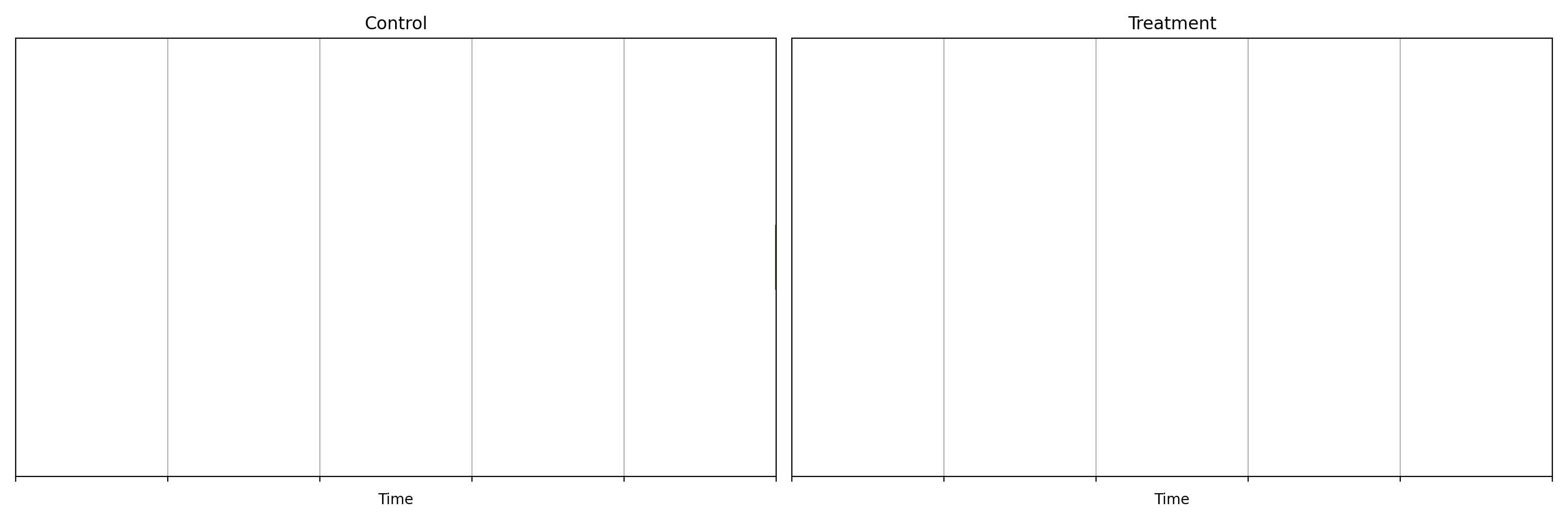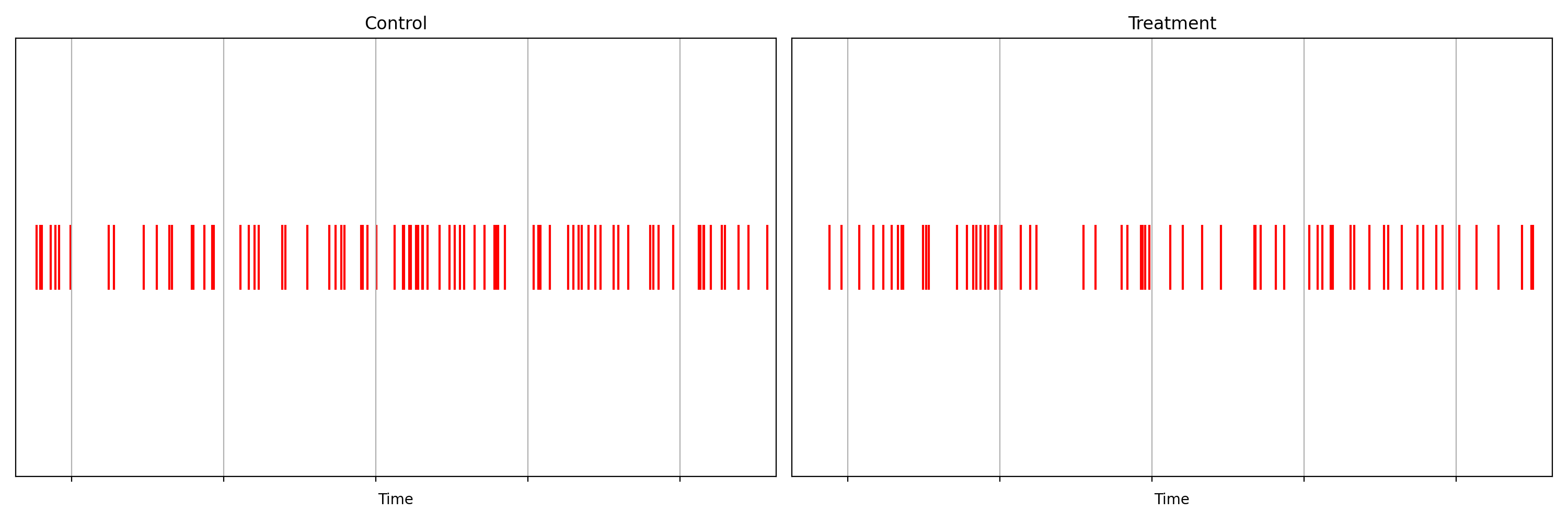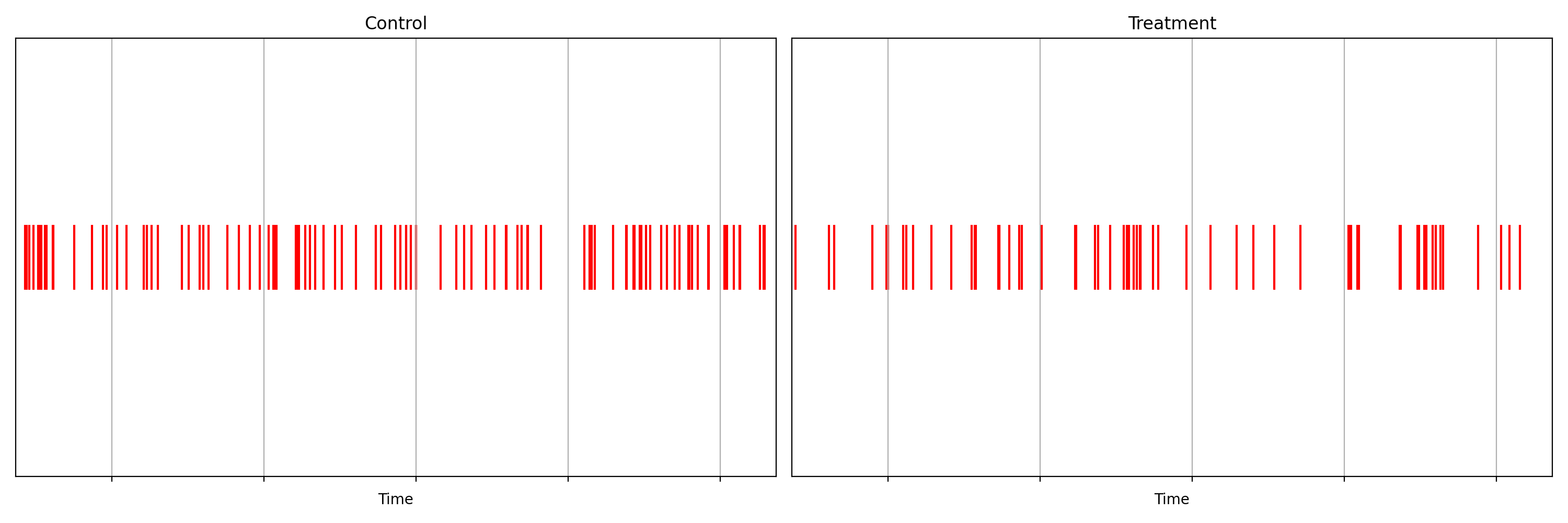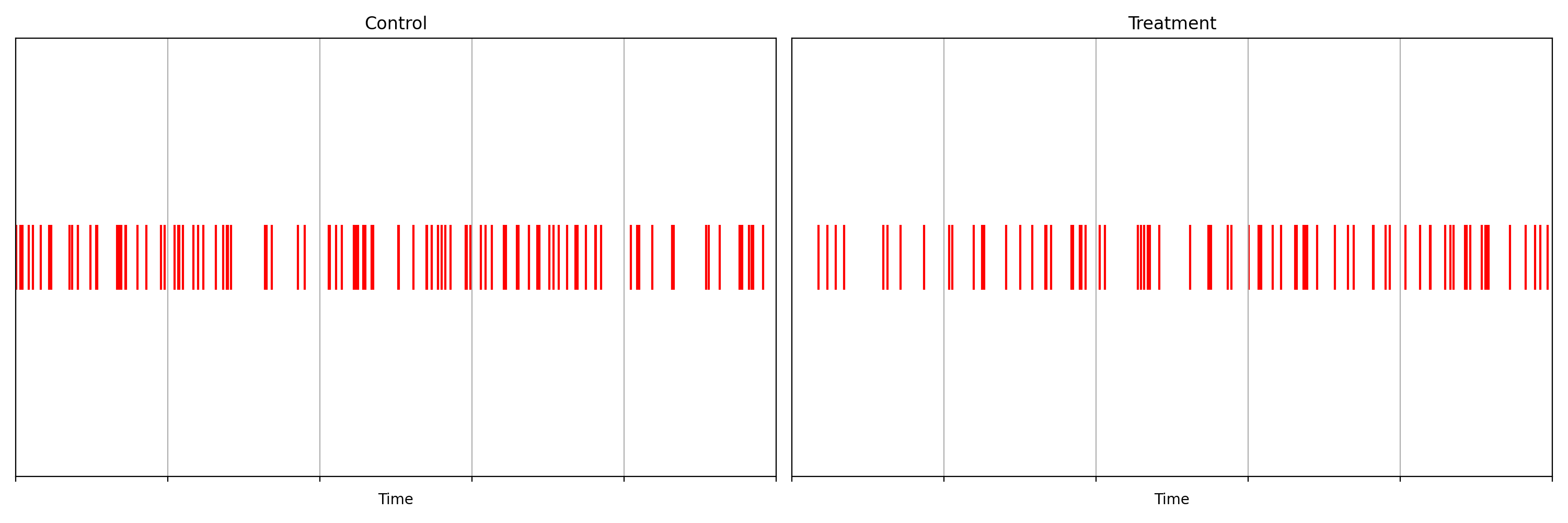
It is not immediately obvious by simple inspection of the point processes in Figure 1. The difference becomes immediately obvious when we visualize the observed counting processes, shown in Figure 2.
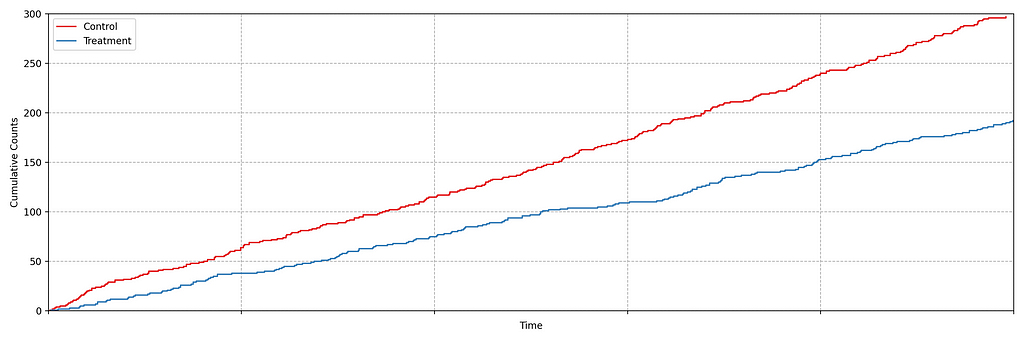
The counting processes are functions that increment by 1 whenever a new event arrives. Clearly, there are fewer events occurring in the treatment than in the control. If these were login events, this would suggest that the new code contains a bug that prevents some users from being able to log in successfully.
This is a common situation when dealing with event timestamps. To give another example, if events corresponded to errors or crashes, we would like to know if these are accruing faster in the treatment than in the control. Moreover, we want to answer that question as quickly as possible to prevent any further disruption to the service. This necessitates sequential testing techniques which were introduced in part 1.
Time-Inhomogeneous Poisson Process
Our data for each treatment group is a realization of a one-dimensional point process, that is, a sequence of timestamps. As the rate at which the events arrive is time-varying (in both treatment and control), we model the point process as a time-inhomogeneous Poisson point process. This point process is defined by an intensity function λ: ℝ → [0, ∞). The number of events in the interval [0,t), denoted N(t), has the following Poisson distribution
N(t) ~ Poisson(Λ(t)), where Λ(t) = ∫₀ᵗ λ(s) ds.
We seek to test the null hypothesis H₀: λᴬ(t) = λᴮ(t) for all t i.e. the intensity functions for control (A) and treatment (B) are the same. This can be done semiparametrically without making any assumptions about the intensity functions λᴬ and λᴮ. Moreover, the novelty of the research is that this can be done sequentially, as described in section 4 of our paper. Conveniently, the only data required to test this hypothesis at time t is Nᴬ(t) and Nᴮ(t), the total number of events observed so far in control and treatment. In other words, all you need to test the null hypothesis is two integers, which can easily be updated as new events arrive. Here is an example from a simulated A/A test, in which we know by design that the intensity function is the same for the control (A) and the treatment (B), albeit nonstationary.
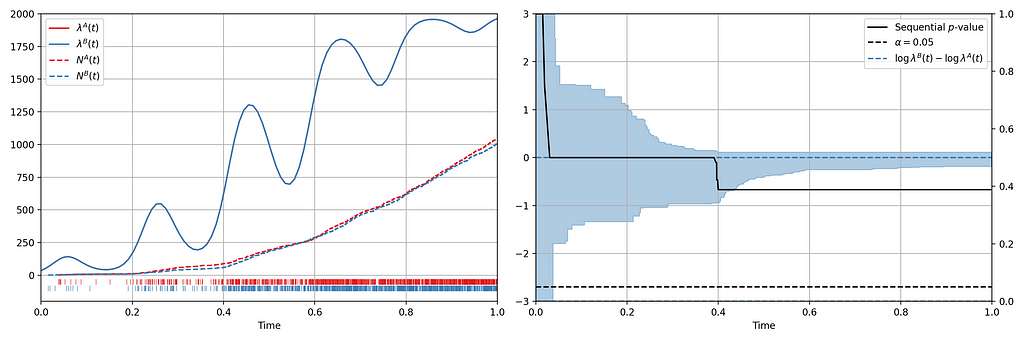
Figure 3 provides an illustration of an A/A setting. The left figure presents the raw data and the intensity functions, and the right figure presents the sequential statistical analysis. The blue and red rug plots indicate the observed arrival timestamps of events from the treatment and control streams respectively. The dashed lines are the observed counting processes. As this data is simulated under the null, the intensity functions are identical and overlay each other. The left axis of the right figure visualizes the evolution of the confidence sequence on the log-difference of intensity functions. The right axis of the right figure visualizes the evolution of the sequential p-value. We can make the two following observations
- Under the null, the difference of log intensities is zero, which is correctly covered by the 0.95 confidence sequence at all times.
- The sequential p-value is greater than 0.05 at all times
Now let’s consider an illustration of an A/B setting. Figure 4 shows observed arrival times for treatment and control when the intensity functions differ. As this is a simulation, the true difference between log intensities is known.
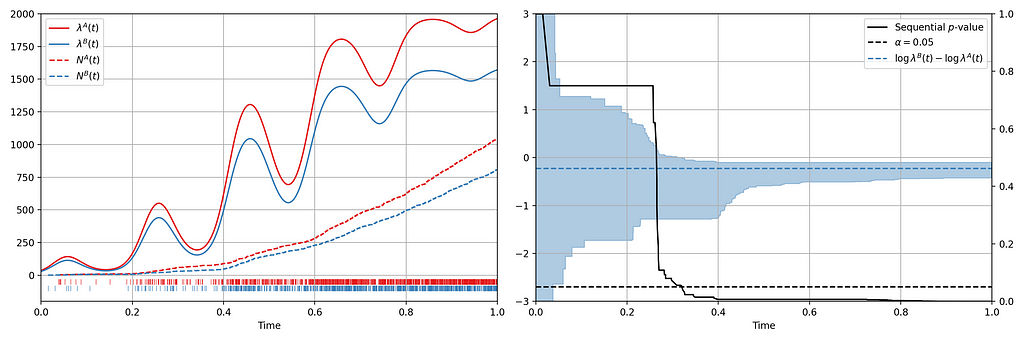
We can make the following observations
- The 0.95 confidence sequence covers the true log-difference at all times
- The sequential p-value falls below 0.05 at the same time the 0.95 confidence sequence excludes the null value of zero
Now we present a number of case studies where this methodology has rapidly detected serious problems in a number of count metrics
Case Study 1: Drop in Successful Title Starts
Figure 2 actually presents counts of title start events from a real canary test. Whenever a title starts successfully, an event is sent from the device to Netflix. We have a stream of title start events from treatment devices and a stream of title start events from control devices. Whenever fewer title starts are observed among treatment devices, there is usually a bug in the new client preventing playback.
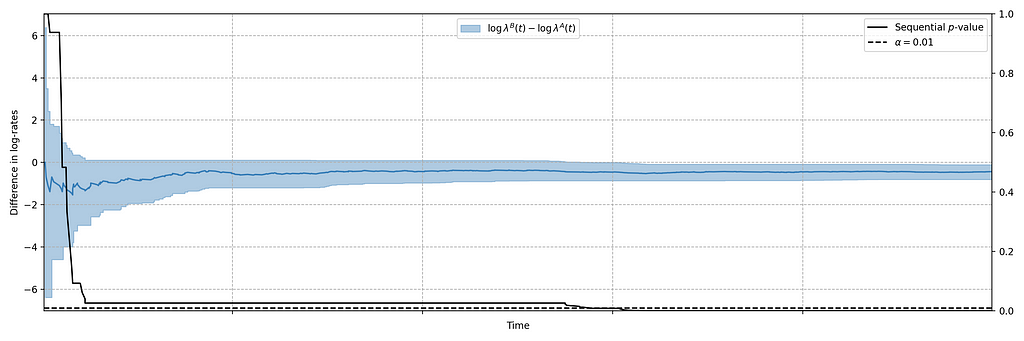
In this case, the canary test detected a bug that was later determined to have prevented approximately 60% of treatment devices from being able to start their streams. The confidence sequence is shown in Figure 5, in addition to the (sequential) p-value. While the exact units of time have been omitted, this bug was detected at the sub-second level.
Case Study 2: Increase in Abnormal Shutdowns
In addition to title start events, we also monitor whenever the Netflix client shuts down unexpectedly. As before, we have two streams of abnormal shutdown events, one from treatment devices, and one from control devices. The following screenshots are taken directly from our Lumen dashboards.
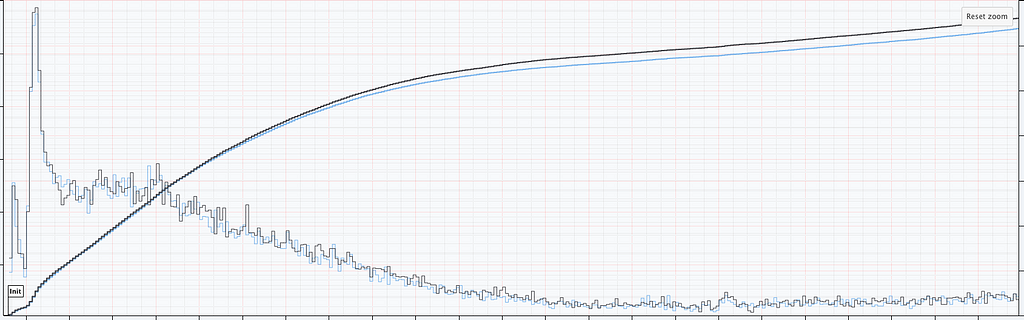
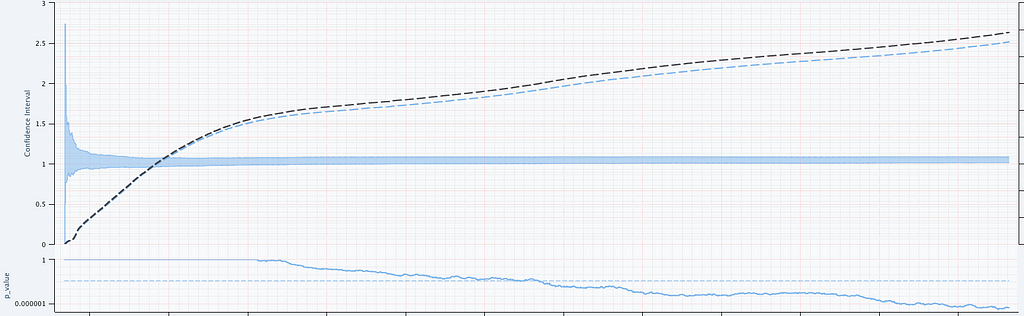
Figure 6 illustrates two important points. There is clearly nonstationarity in the arrival of abnormal shutdown events. It is also not easy to visibly see any difference between treatment and control from the non-cumulative view. The difference is, however, much easier to see from the cumulative view by observing the counting process. There is a small but visible increase in the number of abnormal shutdowns in the treatment. Figure 7 shows how our sequential statistical methodology is even able to identify such small differences.
Case Study 3: Increase in Errors
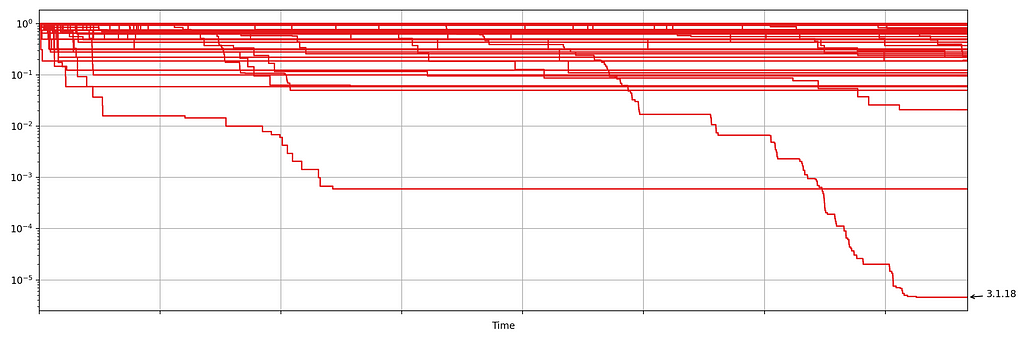
Netflix also monitors the number of errors produced by treatment and control. This is a high cardinality metric as every error is annotated with a code indicating the type of error. Monitoring errors segmented by code helps developers diagnose issues quickly. Figure 8 shows the sequential p-values, on the log scale, for a set of error codes that Netflix monitors during client rollouts. In this example, we have detected a higher volume of 3.1.18 errors being produced by treatment devices. Devices experiencing this error are presented with the following message:
“We’re having trouble playing this title right now”
Knowing which errors increased can streamline the process of identifying the bug for our developers. We immediately send developers alerts through Slack integrations, such as the following
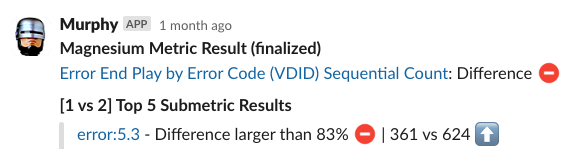
The next time you are watching Netflix and encounter an error, know that we’re on it!
Try it Out!
The statistical approach outlined in our paper is remarkably easy to implement in practice. All you need are two integers, the number of events observed so far in the treatment and control. The code is available in this short GitHub gist. Here are two usage examples:
> counts = [100, 101]
> assignment_probabilities = [0.5, 0.5]
> sequential_p_value(counts, assignment_probabilities)
1
> counts = [100, 201]
> assignment_probabilities = [0.5, 0.5]
> sequential_p_value(counts, assignment_probabilities)
5.06061172163498e-06
The code generalizes to more than just two treatment groups. For full details, including hyperparameter tuning, see section 4 of the paper.
Further Reading
- Anytime Valid Inference for Multinomial Count Data
- Sequential A/B Testing Keeps the World Streaming Netflix Part 1: Continuous Data
Sequential Testing Keeps the World Streaming Netflix Part 2: Counting Processes was originally published in Netflix TechBlog on Medium, where people are continuing the conversation by highlighting and responding to this story.
