Quantum computers promise to solve some problems exponentially faster than classical computers, but there are only a handful of examples with such a dramatic speedup, such as Shor’s factoring algorithm and quantum simulation. Of those few examples, the majority of them involve simulating physical systems that are inherently quantum mechanical — a natural application for quantum computers. But what about simulating systems that are not inherently quantum? Can quantum computers offer an exponential advantage for this?
In “Exponential quantum speedup in simulating coupled classical oscillators”, published in Physical Review X (PRX) and presented at the Symposium on Foundations of Computer Science (FOCS 2023), we report on the discovery of a new quantum algorithm that offers an exponential advantage for simulating coupled classical harmonic oscillators. These are some of the most fundamental, ubiquitous systems in nature and can describe the physics of countless natural systems, from electrical circuits to molecular vibrations to the mechanics of bridges. In collaboration with Dominic Berry of Macquarie University and Nathan Wiebe of the University of Toronto, we found a mapping that can transform any system involving coupled oscillators into a problem describing the time evolution of a quantum system. Given certain constraints, this problem can be solved with a quantum computer exponentially faster than it can with a classical computer. Further, we use this mapping to prove that any problem efficiently solvable by a quantum algorithm can be recast as a problem involving a network of coupled oscillators, albeit exponentially many of them. In addition to unlocking previously unknown applications of quantum computers, this result provides a new method of designing new quantum algorithms by reasoning purely about classical systems.
Simulating coupled oscillators
The systems we consider consist of classical harmonic oscillators. An example of a single harmonic oscillator is a mass (such as a ball) attached to a spring. If you displace the mass from its rest position, then the spring will induce a restoring force, pushing or pulling the mass in the opposite direction. This restoring force causes the mass to oscillate back and forth.
 |
| A simple example of a harmonic oscillator is a mass connected to a wall by a spring. [Image Source: Wikimedia] |
Now consider coupled harmonic oscillators, where multiple masses are attached to one another through springs. Displace one mass, and it will induce a wave of oscillations to pulse through the system. As one might expect, simulating the oscillations of a large number of masses on a classical computer gets increasingly difficult.
 |
| An example system of masses connected by springs that can be simulated with the quantum algorithm. |
To enable the simulation of a large number of coupled harmonic oscillators, we came up with a mapping that encodes the positions and velocities of all masses and springs into the quantum wavefunction of a system of qubits. Since the number of parameters describing the wavefunction of a system of qubits grows exponentially with the number of qubits, we can encode the information of N balls into a quantum mechanical system of only about log(N) qubits. As long as there is a compact description of the system (i.e., the properties of the masses and the springs), we can evolve the wavefunction to learn coordinates of the balls and springs at a later time with far fewer resources than if we had used a naïve classical approach to simulate the balls and springs.
We showed that a certain class of coupled-classical oscillator systems can be efficiently simulated on a quantum computer. But this alone does not rule out the possibility that there exists some as-yet-unknown clever classical algorithm that is similarly efficient in its use of resources. To show that our quantum algorithm achieves an exponential speedup over any possible classical algorithm, we provide two additional pieces of evidence.
The glued-trees problem and the quantum oracle
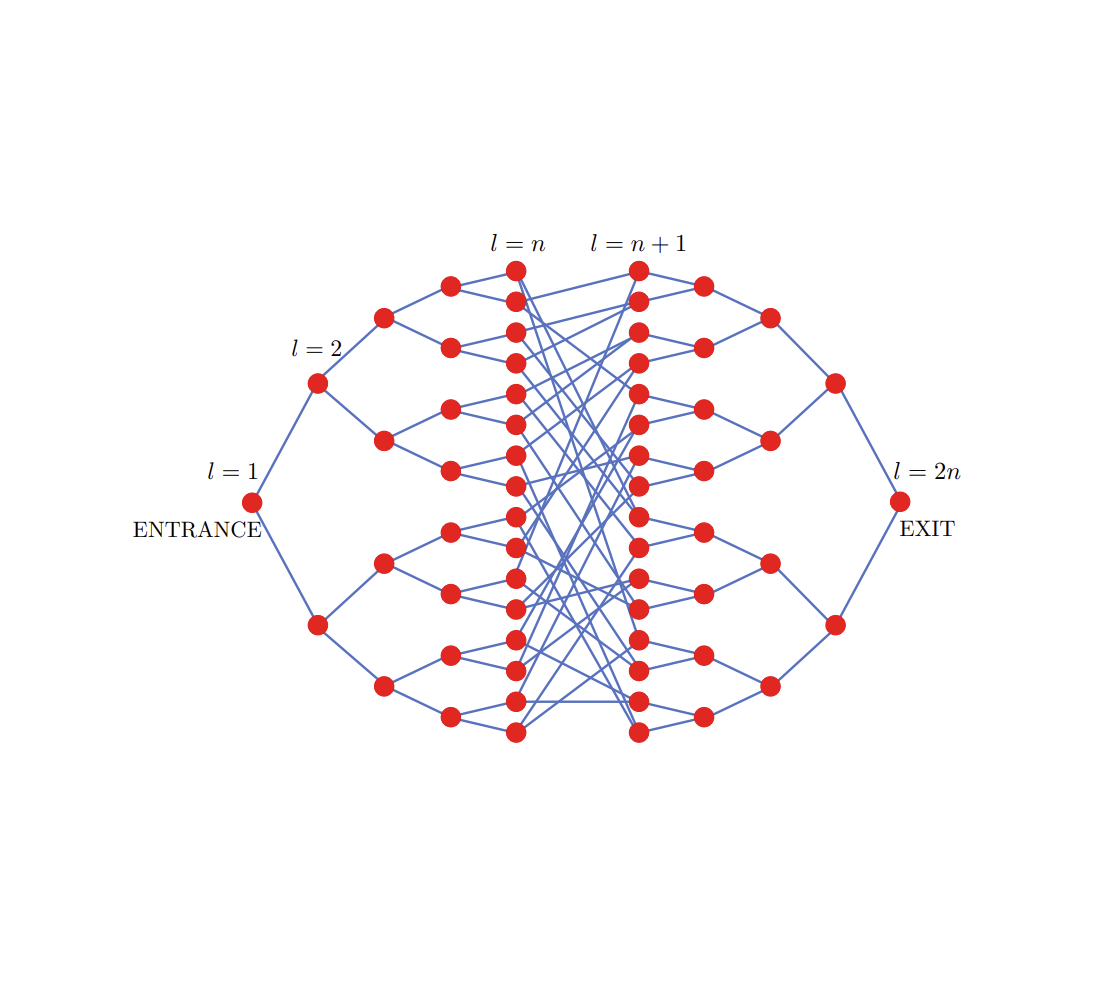
For the first piece of evidence, we use our mapping to show that the quantum algorithm can efficiently solve a famous problem about graphs known to be difficult to solve classically, called the glued-trees problem. The problem takes two branching trees — a graph whose nodes each branch to two more nodes, resembling the branching paths of a tree — and glues their branches together through a random set of edges, as shown in the figure below.
The goal of the glued-trees problem is to find the exit node — the “root” of the second tree — as efficiently as possible. But the exact configuration of the nodes and edges of the glued trees are initially hidden from us. To learn about the system, we must query an oracle, which can answer specific questions about the setup. This oracle allows us to explore the trees, but only locally. Decades ago, it was shown that the number of queries required to find the exit node on a classical computer is proportional to a polynomial factor of N, the total number of nodes.
But recasting this as a problem with balls and springs, we can imagine each node as a ball and each connection between two nodes as a spring. Pluck the entrance node (the root of the first tree), and the oscillations will pulse through the trees. It only takes a time that scales with the depth of the tree — which is exponentially smaller than N — to reach the exit node. So, by mapping the glued-trees ball-and-spring system to a quantum system and evolving it for that time, we can detect the vibrations of the exit node and determine it exponentially faster than we could using a classical computer.
BQP-completeness
The second and strongest piece of evidence that our algorithm is exponentially more efficient than any possible classical algorithm is revealed by examination of the set of problems a quantum computer can solve efficiently (i.e., solvable in polynomial time), referred to as bounded-error quantum polynomial time or BQP. The hardest problems in BQP are called “BQP-complete”.
While it is generally accepted that there exist some problems that a quantum algorithm can solve efficiently and a classical algorithm cannot, this has not yet been proven. So, the best evidence we can provide is that our problem is BQP-complete, that is, it is among the hardest problems in BQP. If someone were to find an efficient classical algorithm for solving our problem, then every problem solved by a quantum computer efficiently would be classically solvable! Not even the factoring problem (finding the prime factors of a given large number), which forms the basis of modern encryption and was famously solved by Shor’s algorithm, is expected to be BQP-complete.
To show that our problem of simulating balls and springs is indeed BQP-complete, we start with a standard BQP-complete problem of simulating universal quantum circuits, and show that every quantum circuit can be expressed as a system of many balls coupled with springs. Therefore, our problem is also BQP-complete.
Implications and future work
This effort also sheds light on work from 2002, when theoretical computer scientist Lov K. Grover and his colleague, Anirvan M. Sengupta, used an analogy to coupled pendulums to illustrate how Grover’s famous quantum search algorithm could find the correct element in an unsorted database quadratically faster than could be done classically. With the proper setup and initial conditions, it would be possible to tell whether one of N pendulums was different from the others — the analogue of finding the correct element in a database — after the system had evolved for time that was only ~√(N). While this hints at a connection between certain classical oscillating systems and quantum algorithms, it falls short of explaining why Grover’s quantum algorithm achieves a quantum advantage.
Our results make that connection precise. We showed that the dynamics of any classical system of harmonic oscillators can indeed be equivalently understood as the dynamics of a corresponding quantum system of exponentially smaller size. In this way we can simulate Grover and Sengupta’s system of pendulums on a quantum computer of log(N) qubits, and find a different quantum algorithm that can find the correct element in time ~√(N). The analogy we discovered between classical and quantum systems can be used to construct other quantum algorithms offering exponential speedups, where the reason for the speedups is now more evident from the way that classical waves propagate.
Our work also reveals that every quantum algorithm can be equivalently understood as the propagation of a classical wave in a system of coupled oscillators. This would imply that, for example, we can in principle build a classical system that solves the factoring problem after it has evolved for time that is exponentially smaller than the runtime of any known classical algorithm that solves factoring. This may look like an efficient classical algorithm for factoring, but the catch is that the number of oscillators is exponentially large, making it an impractical way to solve factoring.
Coupled harmonic oscillators are ubiquitous in nature, describing a broad range of systems from electrical circuits to chains of molecules to structures such as bridges. While our work here focuses on the fundamental complexity of this broad class of problems, we expect that it will guide us in searching for real-world examples of harmonic oscillator problems in which a quantum computer could offer an exponential advantage.
Acknowledgements
We would like to thank our Quantum Computing Science Communicator, Katie McCormick, for helping to write this blog post.